Skip to main content

Math.数学公式合集()

WARNING

以下方法除特殊说明，不传入参数或者传入一个不能转换成数字的参数均返回 NaN， 当然尽量不要这么做。

Math.exp()​

语法​

exp(x: number): number;

描述​

返回以 $e$ 为底的 x 次幂，即计算 $e^x$.

示例​

Math.exp(-1) // 0.36787944117144233

Math.log()​

语法​

log(x: number): number;

描述​

返回一个数的自然对数，即计算 $lnx$.

  • 真数为负数时返回 NaN

  • 真数为 0 时返回 -Infinity

示例​

Math.log(-1) // NaN
Math.log(0) // -Infinity
Math.log(1) // 0
Math.log(10) // 2.302585092994046

下面的函数返回以 x 为底 y 的对数，即计算 $log_x^y$.

function getBaseLog(x, y) {
  return Math.log(y) / Math.log(x)
}

// IEEE-754 精度问题
getBaseLog(10, 1000) // 2.9999999999999996

Math.log10()​

语法​

log10(x: number): number;

描述​

返回一个数字以 10 为底的对数，即计算 $log_{10}^x$

示例​

Math.log10(1) // 0
Math.log10(100) // 2

Math.log1p()​

语法​

log1p(x: number): number;

描述​

返回一个数字加 1 后的自然对数，即计算 $ln(x + 1)$.

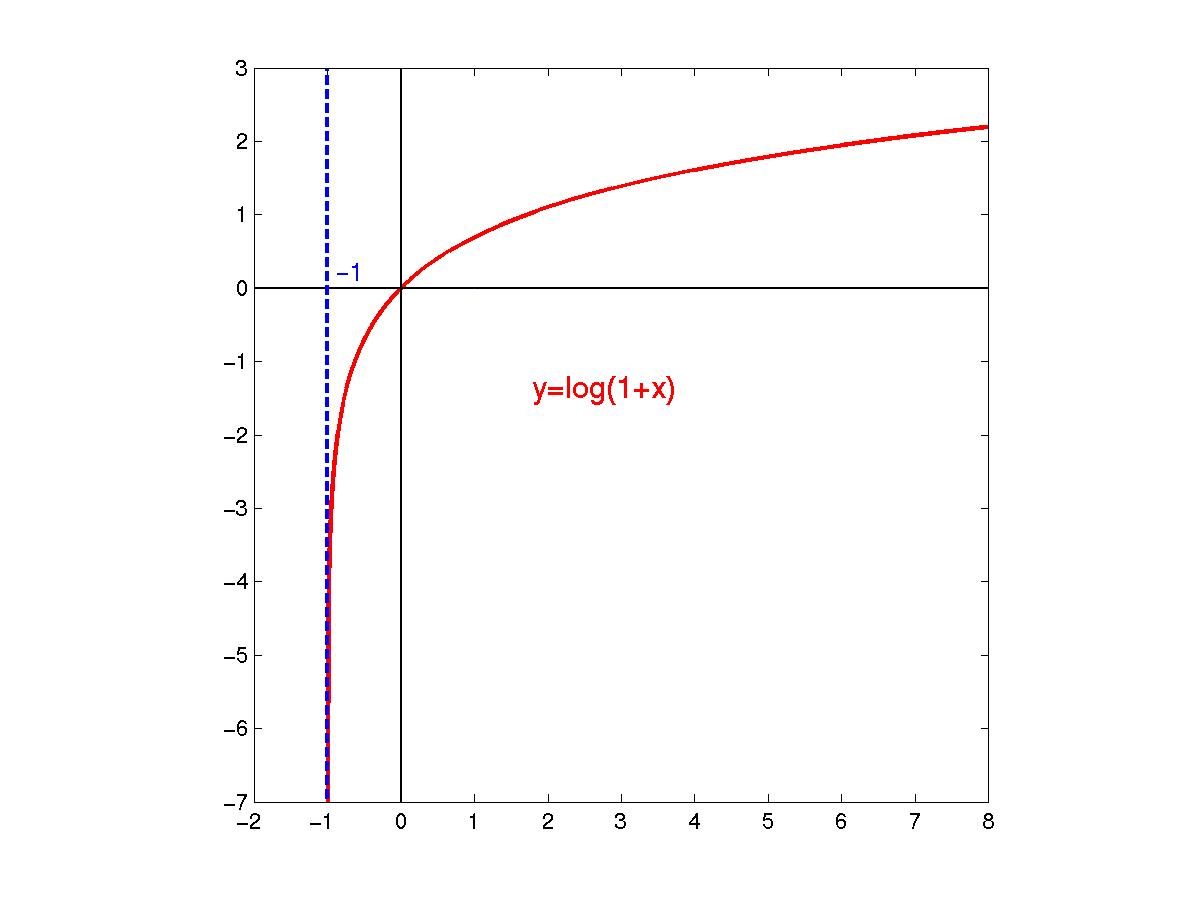
Math.log1p

示例​

Math.log1p(Math.E - 1) // 1
Math.log1p(Math.pow(Math.E, 2) - 1) // 2.1269280110429722

Math.log2()​

语法​

 log2(x: number): number;

描述​

返回一个数字以 2 为底的对数，即计算 $log_2^x$.

示例​

Math.log2(1024) // 10
Math.log2(1) // 0

Math.sqrt()​

语法​

sqrt(x: number): number;

描述​

返回一个数字的平方根，即计算 $\sqrt{x}$.

示例​

Math.sqrt(1) // 1
Math.sqrt(0) // 0
Math.sqrt(-1) // NaN
Math.sqrt(1024) // 32

Math.cbrt()​

语法​

cbrt(x: number): number;

描述​

返回任意数字的立方根，即计算 $\sqrt[3]{x}$.

示例​

Math.cbrt(1) // 1
Math.cbrt(0) // 0
Math.cbrt(-1) // -1
Math.cbrt(512) // 8

Math.pow()​

语法​

pow(x: number, y: number): number;

描述​

返回 x 的 y 次幂，即计算 $x^y$，不传入参数或只传入一个参数均返回 NaN

示例​

Math.pow(2, 4) // 16
Math.pow() // NaN
Math.pow(2) // NaN

Math.hypot()​

语法​

hypot(...values: number[]): number;

描述​

返回所有参数的平方和的平方根，即计算 $\sqrt{\sum\limits_{i=1}^{n} v_i^2} = \sqrt{x_1^2 + x_2^2 + ... + x_n^2}$

  • 当不传入参数时返回 0 （特例）

  • 可以传入一个负数，因为平方时被转换成了正数

示例​

Math.hypot(3, -4) // 5
Math.hypot() // 0

Math.expm1()​

语法​

expm1(x: number): number;

描述​

返回 $e^x - 1$，其中 x 是传入的参数。

示例​

Math.expm1(0) // 0
Math.expm1(1) // 1.718281828459045